J’ai testé pour vous – Résoudre les problèmes avec la modélisation du CE2 au CM2 des éditions Hachette

Bonjour à tous !

Je profite de ce début de vacances pour me replonger un peu dans mon blog et mes réflexions pédagogiques. Pour les lecteurs qui auraient suivi mon parcours, je suis de retour en élémentaire depuis l’an dernier où j’enseigne dans une classe de CE2. J’assume également les fonctions de directrice d’une école de 5 classes.

Après 8 ans en maternelle, il m’a fallu me replonger dans les programmes de l’élémentaire (depuis ma classe unique, le CE2 est passé dans le cycle 2 alors qu’à l’époque, il était encore au cycle 3 )! Et bien sûr, après cette première année, nous avons eu droit à de nouveaux programmes !

Mes collègues de cycle 2 (CP et CE1) travaillent avec la méthode MHM mais pour ma première année de retour en élémentaire, j’ai préféré utiliser une ressource que je connaissais bien. J’ai donc fait le choix de travailler avec Maths au CE2 des édition Accès et de suivre la méthode Résoudre des problèmes au CE2 de chez Retz (méthode qui avait fait ses preuves avec mes élèves lorsque j’étais en classe unique).

La méthode de Retz, en ce qui concerne la résolution de problèmes, est vraiment très efficace. Cependant, elle date de la fameuse période où le CE2 faisait encore partie du cycle 3. Elle est donc au-delà du programme sur pas mal de point. Cependant, j’avais un groupe-classe assez performant et, avec quelques adaptations, ils ont tout à fait pu suivre cette méthode. Petit bémol sur les supports vraiment tristes et peu adaptés à une utilisation directe sur la fiche. Depuis, Retz a sorti les fichiers accompagnant la méthode, mais forcément, cela a un coût et je ne pouvais pas me le permettre !

Par souci d’harmonisation, j’ai rejoint mes collègues cette année en me lançant dans la méthode MHM (chouette, l’année bâtarde où il n’y a pas de version avec les nouveaux programmes pour le niveau CE2 – en dehors de ce qui allait être publié au fil de l’année !). Après un temps de prise en main de la méthode, je prends plaisir à travailler avec et les élèves aussi. J’apprécie la place importante donnée à la manipulation (dont de nombreux élèves de ma classe de cette année ont besoin), les séances en ateliers et les jeux (hyper motivants pour les élèves !), le travail sur les stratégies de calcul mental (que je fais en plus de mes séances de calcul mental en ceintures). Petit bémol, c’est une méthode qui demande un excellent niveau de maitrise dans le domaine des mathématiques car les activités sont très peu détaillées et il faut réellement avoir pris le temps de s’imprégner des principes pédagogiques de la méthode. Pour le coup, la méthode d’Accès est bien plus riche sur le détail des séances, l’aspect didactique et pédagogique.

Mais revenons-en à l’objet de cet article. La résolution de problème a une place importante (et elle le sera encore plus dans l’édition 2026) mais malgré tout, je n’y retrouvais pas ce que j’aimais dans la méthode de Retz pour ce qui est de ce domaine. En observant les résultats de nos cohortes d’élèves du CP au CE2 aux évaluations nationales, il ressortait d’ailleurs très clairement que le niveau chutait d’année en année de façon assez spectaculaire (avec une remontée pour la cohorte étant passée par la méthode de Retz !). J’étais donc bien décidée à creuser la question pour les prochaines années, réflexion que nous mèneront bien entendu en équipe également.

C’est là que je me suis souvenue que, lorsque j’étais encore en maternelle, Hachette m’avait envoyé un spécimen de son ouvrage « Résoudre les problèmes avec la modélisation du CE2 au CM2 ». Je l’avais feuilleté rapidement, puis mis de côté, ne pouvant de toute façon pas le tester en classe à l’époque.

Je l’ai donc ressorti de mes étagères pour le potasser pendant ces vacances, en projection de l’année prochaine. Quel bien m’en a pris ! Il allie ce que j’aimais dans la méthode de Retz (travailler de façon spécifique les types de problèmes), la pédagogie explicite, la modélisation par l’utilisation du modèle en barre (issu de la méthode de Singapour) et la mise en œuvre d’un plan de résolution (avec des petites mascottes trop mignonnes qui me rappellent mes Mystik’s). Bref de quoi équiper les élèves pour devenir des champions de la résolution de problème.

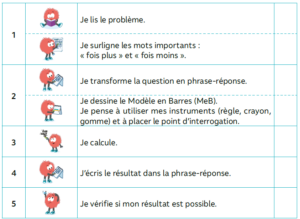
La méthode se découpe en 6 séquences de chacune 6 séances. La première séquence est vraiment centrée sur l’élaboration d’un programme de résolution (accompagné d’une grille de relecture pour les élèves) : elle met en avant l’importance de commencer la résolution du problème (après lecture de l’énoncé bien évidemment) par la rédaction de la phrase-réponse. En effet, cela permet de « fixer son attention sur l’inconnue à rechercher. J’ai d’ailleurs beaucoup aimé celle du défi du problème sur les dinosaures à résoudre en « 6 minutes et 22 secondes ». Si les élèves ne prennent pas le temps de réfléchir à la phrase-réponse en amont, ils vont se lancer dans une série de calculs qu’ils ne pourront pas résoudre dans le temps imparti. La réponse à la question étant déjà écrite dans l’énoncé, aucun calcul n’est nécessaire. Cela permet aux enfants de comprendre l’importance de commencer par l’étape de transformation de la question en phrase-réponse ! On ne parle pas encore de modélisation en barre à cette étape, mais uniquement de schématisation/dessin.

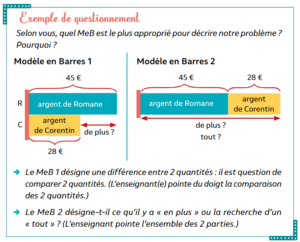
C’est à partir de la séquence 2 que nous commençons à aborder la modélisation en barres, avec la résolution de problèmes « tout et partie » (recherche du tout, avec l’addition, ou recherche d’une partie, avec la soustraction).

Le programme de résolution conserve une trame identique mais est complété au fil des séquences et des types de problèmes abordés :

Concernant la progression, l’ouvrage en propose 2 : une répartie sur 3 ans et une répartie sur 1 an. Cela reste à tester bien entendu, mais je pense mettre en œuvre les 5 premières séquences sur ma classe de CE2. L’idée serait que les élèves conservent les programmes de résolution pour le CM1 et le CM2. Les collègues pourraient alors reprendre les séquences 2 à 5 voire 2 à 6, chaque année, tout en proposant comme support des problèmes relevant du CM1-CM2. Je pense même que les séquences 1 et 2 gagneraient à être découvertes dès le CE1 pour introduire le plus tôt possible cette démarche et l’utilisation du modèle en barres.

Vous l’aurez compris, je suis très emballée par cette méthode et j’ai hâte de la mettre en œuvre (et peut-être même que je testerai les séquences 1 et 2 avec mes CE2 de cette année).

Si vous voulez en découvrir un peu plus, je vous invite à vous rendre sur le site d’Hachette. Ils proposent plusieurs extraits en téléchargement : un extrait du livre, un extrait des photofiches et les propositions de progression du CE2 au CM2.

N’hésitez pas à nous faire part de votre expérience si vous avez déjà travaillé à partir de cet ouvrage dans votre classe, école… Comment vous êtes-vous organisés, comment l’ont vécu vos élèves, avez-vous constaté des progrès ?

Je mettrai cet article à jour après mon année d’expérimentation !